728x90
반응형
뉴런: 정보처리를 하는 가장 최소의 단위
전위가 임계값을 넘으면 다음 뉴런으로 신호를 전달하고, 임계값에 미치지 못하면 아무것도 하지 않음.
파라미터가 뉴런을 비슷하게 흉내낸 것임.
cnn -> 영상처리
rnn -> 자연어처리
퍼셉트론

y= ax + b
y : 출력 a: 가중치 x: 입력
다층 퍼셉트론
ex) xor 연산


가운데 숨어있는 은닉층으로 퍼셉트론이 각각 자신의 w와 b를 알아낼 수 있다.

>> xor 문제의 해결

import numpy as np
# 가중치와 바이어스
w11 = np.array([-2,-2])
w12 = np.array([2,2])
w2 = np.array([1,1])
b1 = 3
b2 = -1
b3 = -1
# 퍼셉트론
def MLP(x, w, b):
y = np.sum(w * x) + b
if y <= 0:
return 0
else:
return 1
# NAND 게이트
def NAND(x1, x2):
return MLP(np.array([x1,x2]), w11, b1)
# OR 게이트
def OR(x1, x2):
return MLP(np.array([x1,x2]), w12, b2)
# AND 게이트
def AND(x1, x2):
return MLP(np.array([x1,x2]), w2, b3)
# XOR 게이트
def XOR(x1, x2):
return AND(NAND(x1,x2), OR(x1, x2))
if __name__ == '__main__':
for x in [(0,0), (1,0), (0,1), (1,1)]:
y = XOR(x[0], x[1])
print("입력 값: " + str(x) + " 출력 값: " + str(y))>> 단일 퍼셉트론으로는 해결되지 않던 문제 (xor 연산)를 은닉층을 만들어 다중퍼셉트론으로 해결
>> 은닉층을 여러개 쌓아올려 복잡한 문제를 해결하는 과정이 뉴런이 복잡한 과정을 거쳐 사고를 낳는 사람의 신경망을 닮음
>> 그래서 이 방법을 인공신경망 이라 부르기 시작했고, 이를 간단히 줄여서 신경망 이라고 통칭한다.
import numpy as np
# 가중치와 바이어스
w11 = np.array([-7.4049234,-7.404924])
w12 = np.array([8.670591,8.670472])
w2 = np.array([7.4178576,7.4178576])
b1 = 11.28
b2 = -3.87
b3 = -11.299384
# 퍼셉트론
def MLP(x, w, b):
# 시그모이드 함수 전체를 사용했으므로 0.5 기준 비교
y = 1/ (1 + np.exp(-(np.dot(w, x) + b)))
if y <= 0.5:
return 0
else:
return 1
# NAND 게이트
def NAND(x1, x2):
return MLP(np.array([x1,x2]), w11, b1)
# OR 게이트
def OR(x1, x2):
return MLP(np.array([x1,x2]), w12, b2)
# AND 게이트
def AND(x1, x2):
return MLP(np.array([x1,x2]), w2, b3)
# XOR 게이트
def XOR(x1, x2):
return AND(NAND(x1,x2), OR(x1, x2))
오차 역전파
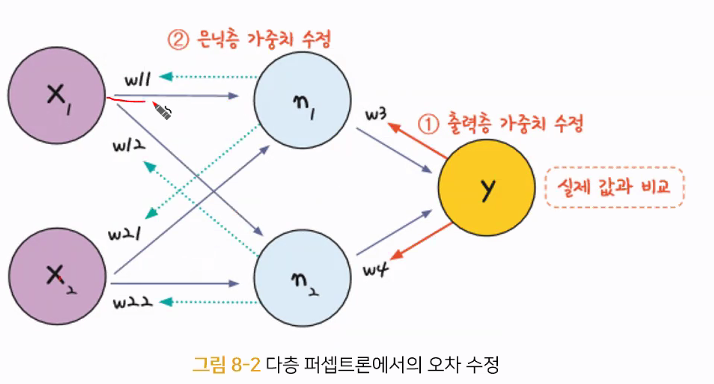
최적화의 계산 방향이 출력층에서 시작해 앞으로 진행된다
>> 오차 역전파
1) 임의의 초기 가중치를 준뒤 결과를 게산
2) 계산 결과와 우리가 원하는 값 사이의 오차를 계산
3) 경사하강법을 이용해 바로 앞 가중치를 오차가 작아지는 방향으로 업데이트 = 미분 값이 0에 가깝도록


>> relu함수가 sigmoid 함수보다 기울기 소실면에서 적은 손실을 보인다
sigmoid > tanh > relu 함수 변천
728x90
반응형
'Deep Learning' 카테고리의 다른 글
| [DL] ONNX (0) | 2024.11.19 |
|---|---|
| 신경망 keras로 접근하기 (0) | 2024.06.05 |
| 시계열 평활기법 - 1 (0) | 2023.09.17 |
| [CV] 색공간 (수정중) (0) | 2023.08.17 |
| [DL] 신경망 (Neural Network) (수정중) (0) | 2023.08.14 |

