Supervised Learning Overview
지도학습 : 문제-정답 쌍이 주어졌을 때, 어떤 문제를 풀도록 학습시키는 것

예시)
- 10가지 카테고리의 이미지를 분류하도록 처리
- 텍스트 문장이 긍정인지 부정인지
- 문장이 완성되지 않았을 때, 다음에 올 단어를 맞추는 것
- 한 언어에 대한 문장을 다른 언어로 번역하여 출력
- 다음날이나 몇시간 뒤의 주식정보, 상승 혹은 하강
>> 문제와 정답 쌍으로 이루어진 데이터를 사용
= x에 대한 y값이 pair형태로 정해짐
예시)
- 이미지가 x로 입력데이터, 분류 클래스 카테고리가 y인 출력데이터가 됨
- x는 텍스트 문장, y는 긍정(1) 혹은 부정(-1)
- 앞 단어가 x 입력이라면, 그 다음에 올 단어를 y
- x는 전 몇일간의 주가 정보, y는 다음날의 주가(실수)
비지도학습 : 문제-정답 쌍이 주어지지 않았을 때, 학습하는 것

이전)
0이라는 손글씨를 판단하기 위해서는
> 곡선으로 이루어짐
> 가운데 구멍이 뚫림
등의 특징으로 설명하려고 함
현재)
>>그러나 이는 사람마다 다른 특징을 지닐수도 있다 = 오차 유발
>> 머신러닝의 접근방식을 따름
= 문제와 정답 쌍을 데이터로 넣으면 스스로 이에 대한 패턴을 학습함
= 컴퓨터가 스스로 학습하게 하고, 규칙을 스스로 파악하게 함 = 머신러닝
정답함수 f*(스타) : 정확하게 문제에 대한 답을 찾아내는 가상의 정답함수
> g(x)를 f*(x)에 가장 가깝게하는 g값을 찾는것
g에서 집합을 몇가지로 추리고, 거기서 정답함수와 가장 근사한 값을 찾음
> 존재하는 모든 함수가 아닌, g라고 하는 함수집합 안에서 찾도록 범위를 좁힘
손실함수를 통해 얼마나 근사한지를 수치화할 수 있음
> n개의 데이터가 주어졌을 때, 나오는 오차(loss)값의 합이나 평균값을 계산하여 이를 손실함수(loss function)의 값으로 사용한다.
> 훌륭한 함수 = 정답함수와 유사한 함수 = loss가 작은 함수
ex) 키에 대한 몸무게를 예측
1) 데이터 - x: 키, y: 몸무게

2) 선형함수 = ax + b의 형태
여기서 a와 b를 찾는 문제이다.
> 선형함수 이므로 클래스를 좁혔다.
3) loss값 찾기
실제값과 예측값 간의 차이를 오차로 두고
이 오차의 제곱한 값의 평균값(mse)을 loss값으로 한다.

>> 우리는 흔히 x와 y를 구하는 문제를 풀지만
여기서는 x와 y는 우리가 가진 데이터의 값이고,
a와 b의 값이 우리가 구하고자 하는 변수가 된다
Linear Regression
다차원 선형회귀
x: x1, x2, x3, ... , xd 와 y값을 가짐
이를 선형 회귀로 나타내면
y= aTx + b
= a1x1 + a2x2 + a3x3 + ... + adxd + b
L(a1, a2, a3, ... , ad, b) : d차원의 a의 벡터와 1차원의 b벡터
= L(1, a1, a2, a3, ... , ad) = a0x0 + a1x1 + a2x2 + ... + adxd (a0 = 1)
= x0 + a1x1 + a2x2 + ... + adxd가 되므로 x0를 b값으로 사용해도 된다.
그러면 d+1차원의 벡터 하나로 정리할 수 있다.

벡터에 대한 미분 (a에 대하여 미분)

> 쉽지만 복잡한 각 편미분 방식으로 풀지 않고도 벡터에 대한 미분으로도 풀 수 있다.
이차항 선형회귀

> y= b+ a0x + a1x^2 의 형태를 띄는 곡선이다.
이는 a와 b에 대한 2차식이 아닌 x와 y에 대한 2차식이 된다. 앞서 설명한 것 처럼 우리는 a와 b에 대해 구하고자 하는 것이기 때문에 이는 1차식으로 표현되어있고, 이 역시 선형회귀로 문제를 풀게 된다.

오버피팅을 방지 > 데이터가 많으면 된다
데이터가 많이 주어지리라는 법은 없고, 데이터를 추가적으로 구하는 것이 불가능 할 수도 있기 때문에 사실 모델이 필요이상으로 복잡해지지않도록 오버피팅 되지 않도록 하는 것이 좋다.
언더피팅 : 데이터를 모두 표현하지 못함
예측율 저하
>> 중간을 찾는 것이 중요
>> 훈련데이터를 훈련데이터와 검증데이터로 나누어 사용!
두개의 데이터로 나누어 사용하여 학습에 이용할 경우, 학습데이터로 학습한 결과로 검증데이터로 검증했을 때
만약 학습데이터가 범용적으로 사용되도록 잘 피팅 되었다면 검증데이터의 loss값이 크지 않을 것이다.
→ 학습시 나왔던 loss( train loss )값과 검증시 나왔던 loss (validation loss)값의 차이가 크지 않다면 이는 오버피팅 되지 않았다고 볼 수 있다.
<학습 시 순서>
1) 데이터를 학습데이터와 검증데이터로 나누고
2) 학습하면서 학습오차가 유의미하게 작아지는 지 확인
3) 충분히 학습이 되어 train loss가 작아졌을 때, 오버피팅이 되었는지를 확인해야 함
4) train loss와 validation loss의 차이가 크지 않은가
5) 차이가 클 경우, 오버피팅의 우려가 있다.
- 보통 8:2의 비율로 훈련과 검증 셋을 나누어 사용한다.
- 테스트 셋은 기존의 데이터가 아닌 새로운 데이터를 이용한다.
- 몇차식의 모델을 고르는 것이 좋은가에 대한 고민에 대해서는 '가급적 간단한 모델을 고르자'라는 룰을 보통 따른다.
- 데이터가 적을 경우, 데이터를 증강 시키지 않고 cross validation 방법을 이용할 수 있다.
< 정규화 Normalization>
: loss 값을 최소로 할 때, 데이터 간의 크기 차이를 줄이기 위해 정규화를 진행
오버피팅을 방지한다.
< 증강 Augmentation>
: 데이터를 많이 얻기 어려울 때, 많이 생성하는 방법
이미지 데이터의 경우, 회전/ 이동 등의 이미지에 변화를 주어 데이터를 증강 시키는 방법이 있다.
이미지 본질은 변하지 않되, 데이터의 개수는 증강 시키는 방법
Gradient Descent
loss값의 최소값 찾기
> gradient의 값이 0인 부분을 찾는 것

learning rate
: 방향을 정했을 때, 가파르게 감소하는 방향으로 얼마나 많이 이동할 것인가
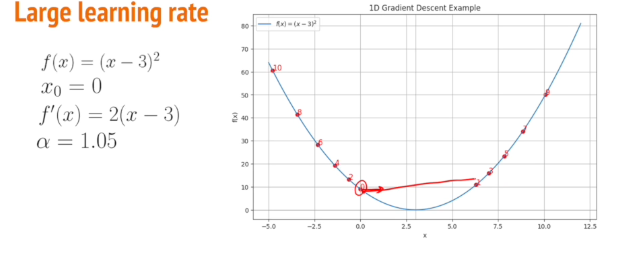
> 큰 learning rate의 경우, 빠르지만 정확한 값으로 수렴하지 못하고 발산할 수 있다.
> 작은 learning rate의 경우, 느리지만 정확한 값을 찾을 수 있다.

loss함수값의 최소값을 찾는 것이 결과적으로 원하는 것!
> gradient를 사용하면 각 데이터마다의 gradient를 계산해서 평균을 낸 것이 전체 gradient가 된다. 이를 이용해서 세타를 업데이트 하는 것이 gradient 알고리즘이 된다!
그러나 이는 n(데이터의 개수)번의 업데이트 연산이 필요하게 된다.

그래서 데이터 포인터 중 하나의 데이터 포인터를 랜덤으로 뽑아 이를 이전에 평균 gradient에 적용하는 것 대신 적용하여 사용하게 된다.
> 그러면 1번의 연산만을 사용하게 된다.
>> 실제 gradient 알고리즘을 사용하지 않기 때문에, 잡음이 있는 형태가 나타날 수 있다. 이는 모든 데이터 포인터가 비슷한 gradient값을 가진다는 가정하에 사용된다.
그러나 데이터 별로 들쭉날쭉할 확률이 높다.

이는 데이터를 하나만 뽑는 것이 아니라 미니배치의 사이즈인 b개의 값만 뽑아서 계산한다.
뽑은 b개에 대한 평균을 구해 업데이트 한다.
>> 가장 많이 사용하는 방법!
gradient descent는 global 한 minimum이 아니고, local minimum 을 구하는 제한된 방안이다.
<이를 보안한 방법> : global minimum을 구하기
momentum SGD : 공을 산에서 굴리는 듯한 sgd 방법. 관성을 주어 지나온 모든 부분에 대해서 계산할 수 있음
RMS Prop : 각 gradient 값을 정규화 해준다
ADAM : 1차원 모멘텀 / 2차 모멘텀의 계산?
'LG Aimers' 카테고리의 다른 글
| [LG AI] 딥러닝 - BackPropagation (0) | 2024.07.25 |
|---|---|
| [LG AI] 지도학습 - 2 (1) | 2024.07.24 |

