[LG AI] 지도학습 - 2

Classification

binary 데이터를 linear 분류하기

 

x값이 2개인 2차원 입력데이터에 따른 binary 분류 그래프

 

Linear Classification 선형분류기

: 선형그래프를 기준으로 0보다 큰지 작은지 나누어 이진분류

> 0-1 손실함수를 사용

 

이 선형 그래프를 어떻게 찾을 것이냐?

> 퍼셉트론 알고리즘 : 데이터가 존재할 때 임의로 선을 긋는다. 이에 계속되는 데이터에 대해 업데이트 된다.

gradient를 계산할 필요가 없다. 하지만 선형으로 분류되지 않는 경우에는 이 선형을 찾는 동작이 무한으로 동작한다.

 

> Linera Programming

 

> SVM (Support Vector Machine) : 선형분류기로부터 각 클래스의 가장 가까운 데이터와의 거리를 'margin(마진)' 이라고 하는데, 이 마진값의 크기가 큰 선형 분류기를 고른다.

 

> Sotf-margin SVM : 완벽하게 선형분류가 되지 않는 경우, 최소한의 데이터만 선형분류기를 넘어가도록 한다.

왼쪽이 C값이 클 때, 오른쪽이 C값이 작을 때

> Hinge Loss : C값이 크다는 건, 잘못 분류된 값에 대해 크게 받아들인다는 것이고

                        C값이 작다는 건, 잘못 분류된 값에 대해 작게 받아들인다는 것이다.

그림으로 다시 설명하면 왼쪽에 C값이 큰 경우에는 전체적인 마진값을 작게 만들기 위해 분류는 잘못된 데이터가 많지만 분류기에서 멀리 떨어지지 않았고,

오른쪽에 C값이 작은 경우에는 분류 자체를 얼마나 잘 했는가에 더 초점을 두고 오분류에 최소를 두고 분류한 모습이다.

 

 

 

 

Logistic Regression

 

Hard Guess

x에 대한 정답 레이블이 1 혹은 -1 과 같이 특정 클래스를 예측하는 것으로 분류됨

Sotf Guess

x에 대한 정답 레이블로 각 클래스에 대한 예측 확률로 표현. 그래서 가장 높은 확률을 가진 클래스를 예측하는 것으로 함

> 1이라고 예측하는 확률과 -1이라고 예측하는 확률, 두가지 실수 출력값으로 이루어짐

 

>> Logistic Regression : 분류를 regression문제로 바꿔서 해결

 

Cross Entropy Loss : 정답에 얼마나 높은 확률로 예측했는가 (ex. 70%의 확률로 비가 올 것이라 예측했는데, 실제로 비가 왔다 = log 1/0.7 (작은 loss), 30%의 확률로 비가 올 것이라고 예측했는데, 실제로 비가 왔다 = log 1/0.3 (높은 loss) )

 

> 확률 분포 사이의 거리를 기반으로 계산

 

 

1) 데이터 준비

2) 함수클래스 준비 : 로지스틱 함수

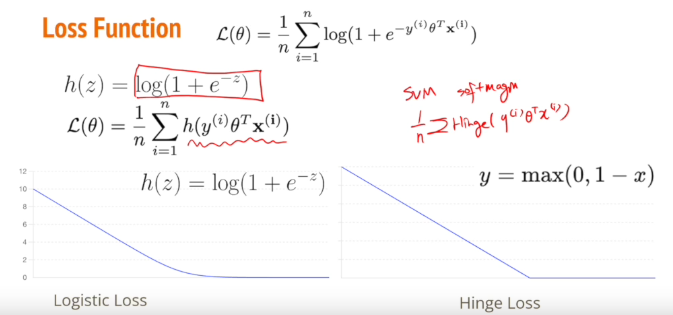
> 로지스틱 회귀에서의 로지스틱 손실함수는 Hinge Loss와 그래프와 식이 유사하지만, 미분 불가능한 부분이 부드럽게 바뀐 모양이라고 생각해도 무관하다.

 

3) 손실함수 : cross entropy loss

 

 

만약 multiclass classification 의 경우라면!

 

모델 예측시, x에 대한 입력에 대해 y클래스를 하나만 예측하는 것이 아니라, 각 클래스에 관해 예측하고자 하는 확률을 출력한다. 이때는 linear regression이 아닌, softmax 함수를 사용한다.

 

> softmax : exponential 를 취하여 정규화 해주면 각 확률이 0보다 큰 양수값을 가지게 되는데, 이 각 클래스에 대한 모든 확률값의 합은 1이 된다.

 

 

 

 

 

More On  Supervised Learning Beyond

 

- 나이브 베이즈

스팸필터 : 각 단어들에 대해 스팸인지 아닌지를 판단

스팸일때 이 단어가 등장할 확률, 스팸이 아닐 때 이 단어가 등장할 확률을 계산하고 확률의 역산을 이용하여 나이브베이즈 정리를 이요하여 계산

 

 

 

 

- 배깅

여러 트리모델을 이용하고, 트리마다 평가를 하고 이 평가를 종합해서 출력을 결정 > 편향되지 않은 결정 가능

 

- 랜덤포레스트

각 트리의 결과를 종합하여 대다수의 트리가 가리키는 클래스를 최종 클래스로 출력한다.

회귀의 경우는 각 트리 결과를 종합하여 평균을 최종 출력으로 결정한다.

 

- ada boost

트리 모델을 독립적으로 순차적으로 학습시켰다고 할때, 첫번째 학습에서 잘못 분류/예측 에는 높은 가중치를 주고 이를 반영하여 두번째 트리에서 학습을 하고 이렇게 순서대로 가중치가 쌓이게 되어 업데이트 하게 된다.

>> 분산을 줄이는 배깅 방법, 점점 성능이 좋아지지만 오버피팅의 문제가 있는 부스팅 방법