[선형대수학] 5주차 0812 (수정중)

수직 기저?

Orthonormal Basis

양변에 임의의 q벡터를 내적

 

Ci = qi^(T) * Y

(qi 벡터의 스칼라값)

>> 선형결합 식에서 특정 벡터의 상수값을 구하고 싶을때, 그 특정 벡터를 양변에 내적해주면

스칼라값을 구할 수 있다.

 

 

그랑슈미트 ( Gran-Schmidt )

; 정사영을 통한 프로제션한 벡터와 기존벡터간의 관계가 수직이다.

=> 길이가 뭐한걸 만들자?

= A3 (a3벡터를 q1,q2 평면에 수직으로 내리는 벡터

basis 벡터를 동일한 공간에서 추출한다고 해도 추출하는 순서가 다르면 다르다(?)

(맨위 필기 Given a1, a2, a3, ... )

 

 

 

 

 

 

 

함수공간 ( Funcion Space )

내적

 

서로 Orthogornal 하다

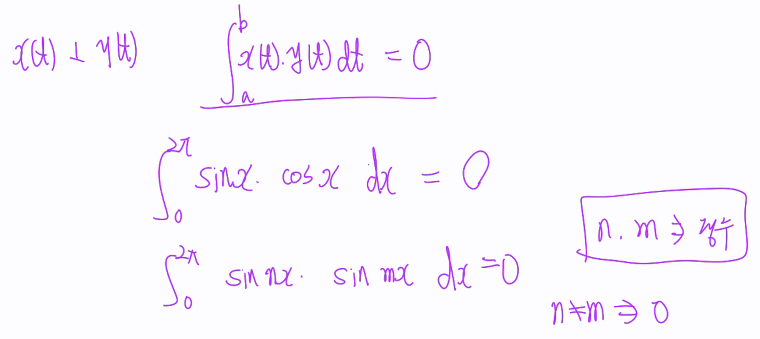
=> Fourier Series!

 

 

 

 

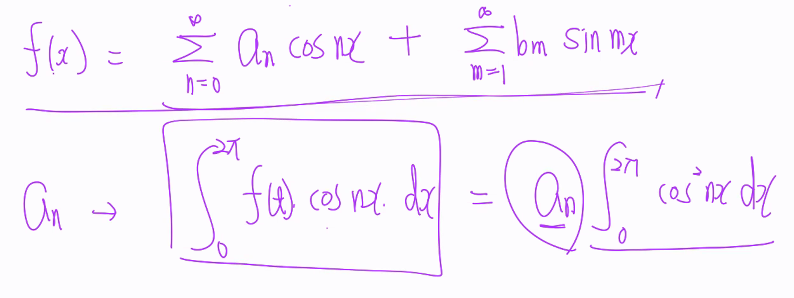
판별식 ( Determinant )

Det(A) 

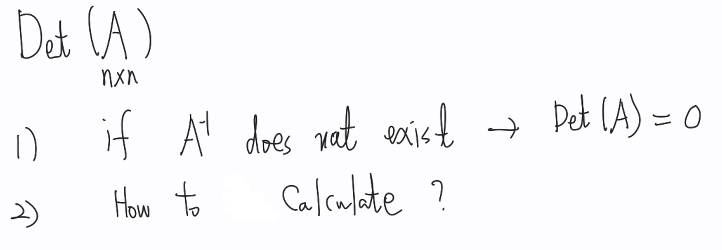
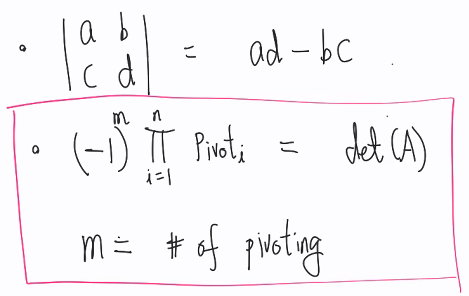
가우스 소거법 후 이어지는 피봇팅의 곱??

 

[ 2 1 4 ]

[ 0 -2 3]

[ 2 1 3 ]

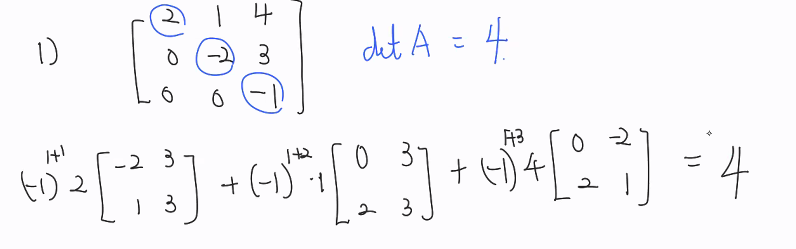
>> 두가지 방법

1) 가우스 소거법

2) 

 

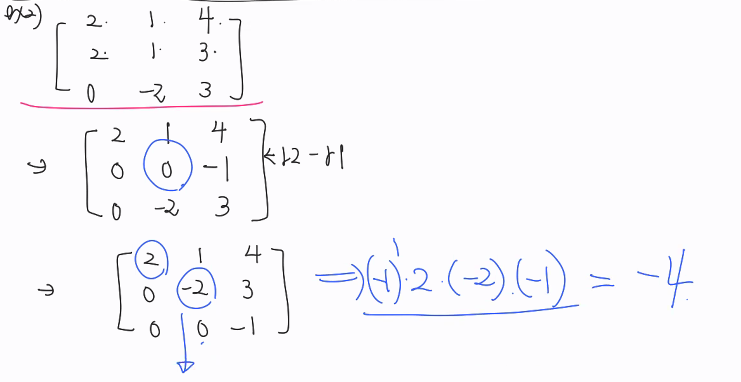
피봇팅의 횟수에 따라 -1를 곱해준다

> 판별식 값이 -4가 나옴!

 

 

 

Eigenvalue & Eigenvector

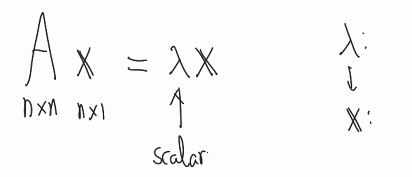
[ 아이젠] 값과 [아이젠] 벡터??