

가우스 소거법 후

피봇의 위쪽값을 1이 되도록 만들기 = upper triangle 부분이 0이 되어야 하는거 아닌교,,

피봇이 있는 칼럼과 없는 칼럼을 구분-> 1,3번 열

-> 이와 같이 식으로 계산하여 미지수 계산
(x,y,u,v)의 4x1의 벡터를 구하고자 함

v의 식으로 표현


벡터 집합이 평행 이동


Ax=0의 조건을 만족하는 N(A)
d에 의해서 만들어지는 상수? 행렬이 평행이동???

벡터공간을 선형결합으로 설명
상수항이 더해지는 순간, 공간이라는 것이 깨짐? linear 한것이 깨짐?
<Linearly Independence of vectors>
; 벡터들이 선형적으로 독립되어있다.
x1, x2,,,,xn 벡터가 있을때, (주어진 벡터 모두가 통째로 독립적인 관계인가?O, 서로 독립관계인가?X)
모든 선형계수의 결합은 0(0벡터)이 되어야 한다.
>> 벡터x에 붙은 상수c1, c2, ...값은 모두 0이 되어야 한다 !
>> 벡터x1, x2, ...는 모두 선형 독립
( 각각(1:1)이 아니라 주어진 벡터 전체 집합이 독립성을 갖는다)
= 만약 세개의 벡터가 있으면 두개의 벡터간의 결합으로 나머지 하나의 벡터를 표현할 수 있는가? NO

EX2) 1+2번 캡처 못함. ㅠ
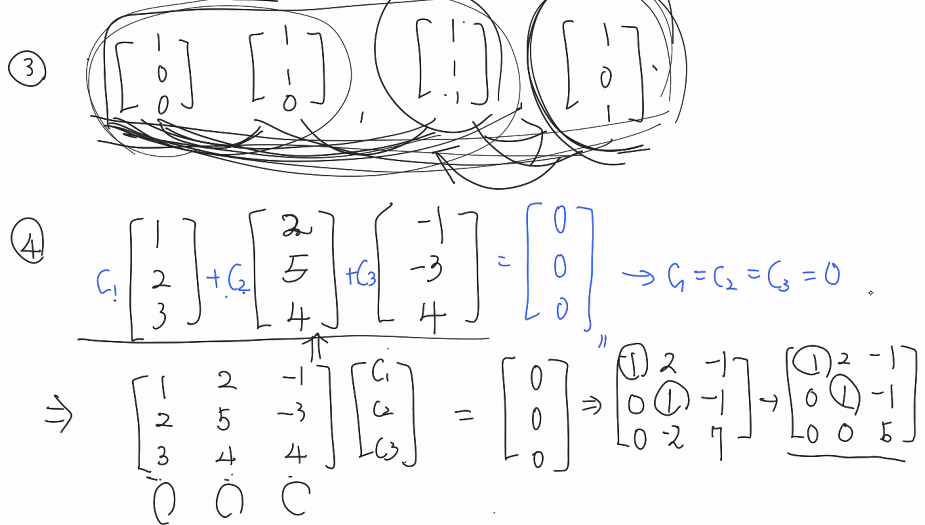
=> 독립인지 안니지를 확인하고 싶은 벡터는 위와 같이 구성하여
가우스소거법 실행 > 대각선방향으로 순서대로
-> 완벽한 UPPER TRIANGLE의 모양으로 만들수 있다.
서로 독립인가? 를 판단하기
① 가우스소거법 (Upper triangle 형태 만들어 주기)
non-zero 피봇에 해당하는 컬럼 벡터들이 선형독립벡터의 집합이고, 그의 개수들이 선형독립벡터의 개수?
(전체 upper triangle 행렬이 만들어 지거나 echelon 행렬이 모든 위치마다 피봇이 non-zero가 될때까지 끝까지 가면 해당 벡터들이 모두 선형독립한 거고 그렇지 않으면 일부만 선형독립한 상태가 됨)
② Q. 독립인가? A. 각 열의 모든 요소가 0이거나 안 친할때..?
<Span>; 구성하다. 만들어내다 음.. 차지하다?
: 기저 벡터공간을 span한다.
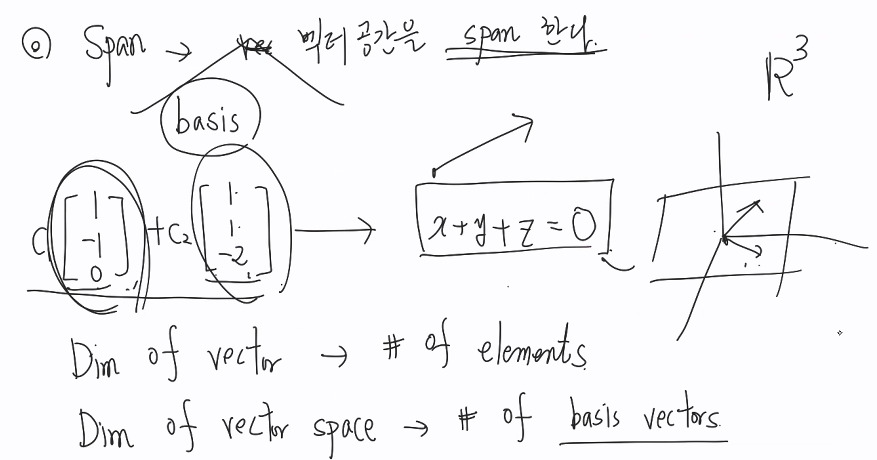
벡터끼리 더하거나 연산해서 새로운 벡터를 만들수 X => 벡터공간 생성
X+Y+Z= 3
<Basis 기저 >
; 벡터 스페이스를 일부/전체를 span하는 벡터들의 집합
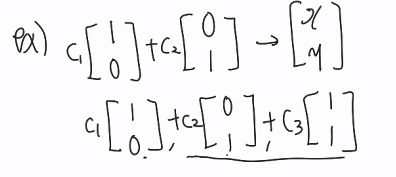
조건① 독립적인 벡터를 가진다.
> 위 식은 성립
> 아래 식은 독립x
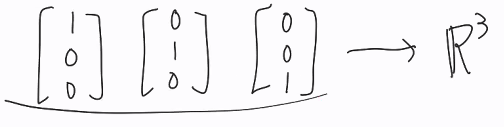
조건② 벡터공간에서 기저 is not unique
> 엥 기저는 unique 해야하는거 아닌가?
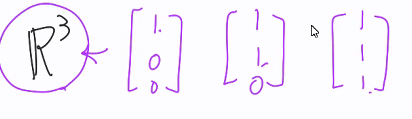
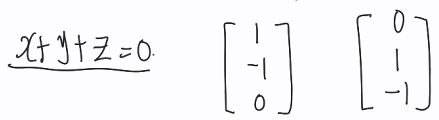
> 규격화 되고 동일한 방법으로 하도록 한 것을 row reduce form?
<4 spaces of matrix Amn>; subspace
① column space C(A)
② null space N(A); x벡터로 이루어진 공간
> 가우시안 소거법? + a =row reduce form. 피봇의 개수= basis의 개수= nullspace의 차원의 수
③ transform C(AT); 행벡터들의 선형결합으로 만들어지는 벡터공간
④ null space N(AT) ; ATy= 0 => (nxm)(mx1) = (nx1)
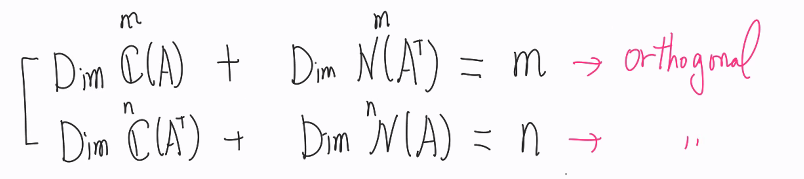
행렬 a를 구성하는 컬럼벡터들 끼리

rank of A = 행렬에서 독립적인 열 벡터(행 벡터)의 수
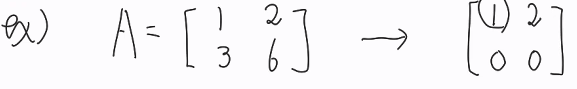
- 컬럼 스페이스 C(A) :
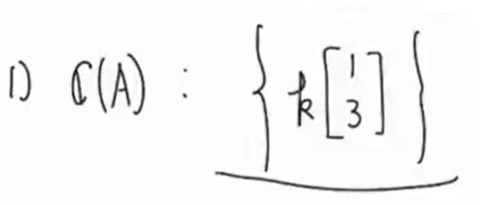
- 로우 스페이스 C(AT) :
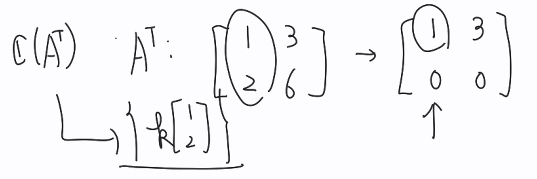
- 널 스페이스 N(A)
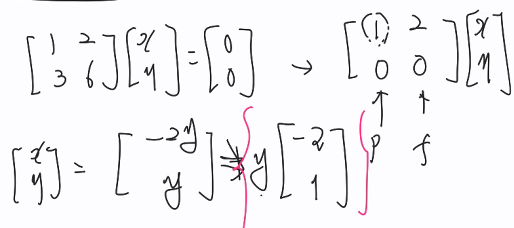
x+ 2y=0
> x= -2y
- left 널스페이스? N(AT)
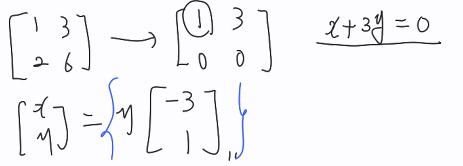
◼Vector Space의 조건
- 벡터들의 집합이다.
원점 ( 0벡터 )을 포함한다.> 벡터 스페이스는 당연히 원점을 포함한다 (조건이라기엔 너무 당연)- 기존 벡터의 덧셈과 스칼라배의 값을 포함한다.
(집합안의 원소끼리의 덧셈이나 스칼라 배의 값이 다시 그 집합의 원소이다.)
⭐행렬4가지의 subspace 조건
- 원점 ( 0벡터 )을 포함한다.
- 기존 벡터의 덧셈값을 포함한다.
(집합안의 원소끼리의 덧셈 값이 다시 그 집합의 원소이다.) - 기존 벡터의 스칼라 배의 값을 포함한다.
(집합안의 원소끼리의 스칼라배 값이 다시 그 집합의 원소이다.)
'선형대수학' 카테고리의 다른 글
| ISLP Chapter 13 Multiple Testing 1 (0) | 2024.04.16 |
|---|---|
| [선형대수] 0819 (0) | 2023.08.19 |
| [선형대수학] 5주차 0812 (수정중) (0) | 2023.08.12 |
| [선형대수학] 4주차 0805 (0) | 2023.08.07 |
| [선형대수학] 2주차 0722 (0) | 2023.07.23 |



